AIL C6 缺省逻辑

非单调逻辑概述

经典逻辑无法处理不确定、不完备、不一致的知识。知识的不完备性在各种基于知识的智能系统中广泛存在。

对于一个知识库的知识的不完备性：存在一个公式，使得依据该知识库不能证明该公式为真，也不能证明该公式为假。

在基于框架的知识表示中，知识的不完备性体现在难以穷尽表示主体的行动对世界状态的影响。

推理系统的非单调性：由在推理系统下推理得到的结论可能会是错误的；出现新信息时，已推出的错误结论允许被收回。

GPT says

非单调逻辑是一种逻辑系统，它允许一些结论在获得新知识或信息之后被撤销或改变。非单调逻辑的分类如下：

1. 缺省逻辑（Default Logic）：这种逻辑基于默认规则，也就是默认情况下可以推断出来的规则。默认规则描述了一些陈述或结论的普遍情况，但是这些陈述或结论可以在获得新信息之后被撤销或修改。缺省逻辑经常用于人工智能和自然语言处理中。
2. 抵制逻辑（Reiter’s Default Logic）：抵制逻辑是缺省逻辑的一种特殊类型，它基于缺省规则和“抵制”规则，抵制规则描述了在某些条件下默认规则不能被应用的情况。
3. 情景逻辑（Situations Logic）：情景逻辑用于描述在不同情境或情景下的推断和结论。情景逻辑中，每个情境都被描述为一组陈述，每个陈述都在某些情境下是真实的。通过切换不同的情境，可以得到不同的结论和推断。
4. 关注逻辑（Relevance Logic）：关注逻辑是一种非常严格的逻辑系统，它要求从一个陈述到另一个陈述的推导必须有明确的逻辑关系。这种逻辑系统强调语句之间的相关性和相关性对于正确推论的重要性。
5. 变迁系统逻辑（STIT Logic）：变迁系统逻辑主要用于描述不同的行动和时间的连续性。它描述了由不同的行动和变迁引起的状态变化，包括物理状态和知识状态，同时描述了这些状态对于行动的影响和反过来的影响。

缺省规则

缺省逻辑由Reiter于 1980 年提出，是一种可以处理例外情况的非单调形式体系：信息的不完备性引起例外情况的存在。

• 缺省推理最基本的特性是暂时性：在缺少信息的情况下推出暂时的结论。该特性是缺省推理研究的核心。
• 缺省推理在本质上是定性的：缺省推理只处理真或假，不处理不确定程度。缺省推理使得相信什么成为可能。

缺省逻辑通过扩充经典逻辑实现对不完备信息的表示与推理。缺省规则是一种特殊的推理规则，缺省逻辑通过使用缺省规则进行扩充。

• 语句：通常情况下，如果$\phi$为真，那么$\psi$为真。

• 表达内容：在没有出现例外的情况下，如果 $\phi$ 为真，那么$\psi$为真。

  “通常情况下”使得这一缺省规则并非在所有情况下都是可应用的。例外情况的出现可以阻止该缺省规则的可应用性。

• 表示：$\phi:\psi / \eta$​ 或者更占空间的

  $$\frac{\phi:\psi}{\eta}$$

• 读作：（三者均可）

  1. 如果可以证明$\phi$，且$\psi$是一致的，那么可以推出$\eta$。
  2. 如果可以证明$\phi$，且不能证明$\lnot\psi$，那么可以推出$\eta$。
  3. 如果可以证明$\phi$，且例外$\lnot\psi$没有发生，那么可以推出$\eta$。

Why we need Default Rules?

• 建模原型推理：“典型地，孩子有父母 ”可以表示为：$C(x):P(x) / P(x)$
• 无风险推理：即使一个结论不是最可能的也可以推出它，因为另一种结论是灾难性的。如无罪推定原则“在没有反面证据时，被告人无罪 ”可以表示为：$A(x):\lnot I(x) / \lnot I(x)$
• 封闭世界假设, CWA：如果一个句子为真，那么知道其为真。当前不知道为真的句子都被假定为假。依据CWA可把一个应用领域描述为一些公理的集合，并以“若一个命题不能从公理
  推出，则它是假的 ”来推理。即表示为：$\top:\lnot\varphi / \lnot\varphi$

缺省规则的形式化定义见缺省逻辑的语法。

缺省逻辑的语法

缺省逻辑的语言

任何 一阶语言都是缺省逻辑的语言。

• 在缺省逻辑中，项，公式等定义与一阶语言里相同。

  RECALL

  项：

  1. 个体常元和个体变元是项。
  2. 如果$t_1,t_2,\cdots,t_n$是项，$f$ 是 $n$ 元函词， 那么 $f(t_1,\cdots , t_n)$ 也是项。
  3. 有限次使用(1)(2)生成的是项。

  公式：

  1. $\rm F(t_1, \cdots , t_n)$是公式，称为原子公式。其中$\rm F$是$n$元关系符号，$\rm t_1, \cdots , t_n$是项。
  2. 如果 $\rm t_1$ 和 $t_2$ 是项，那么 $(t_1 \equiv t_2)$ 是原子公式。
  3. 如果 $\phi$ 和 $\psi$ 是公式，且 $x$ 是出现于 $\phi$ 中的自由变元(可被记为$\phi(x)$)，则 $(\lnot\phi),(\phi \wedge \psi),(\phi \vee \psi),(\phi \rightarrow\psi),(\phi \leftrightarrow\psi),(\forall x\phi),(\exist x\phi)$ 是公式。
  4. 只有有限次使用 (1)(2)(3) 条款生成的符号串才是公式。

缺省规则

一条缺省规则可以被形式化地表示为：

$$\delta = \frac{\varphi : \psi_1,\cdots, \psi_n}{\chi}$$

或表示为

$$\varphi : \psi_1,\cdots, \psi_n/\chi$$

其中，$\varphi,\psi_1,\cdots, \psi_n(n \ge 0)$ 是一阶逻辑公式。

• 公式 $\varphi$：先决条件，也可记作$pre(\delta)$
• 公式$\psi_1,\cdots, \psi_n$ ：缺省条件，也可记作$just(\delta)$
• $\chi$：$\delta$ 的结论，也可记作$cons(\delta)$。特别地，对于缺省规则集合$D$，$cons(D)$可表示$D$中缺省结论集合。

传统逻辑（一阶逻辑）中规则可表示为

$$\frac{\varphi}{\chi}$$

缺省推理规则可以认为是传统规则的“非单调化”。缺省条件中的$\psi_i$ 表示就现有知识而言$\psi_i$ 可能成立(而非必然成立)，$\lnot\psi_i$ 尚未出现。也即在先决条件$\varphi$与结论$\chi$之间存在一定间隙，即单独的$\varphi$的真不能完全确保$\chi$的真。

这种从$\varphi$到$\chi$的推理属于“跳到结论”(jump to conclusion)。

开规则与闭规则

• 开规则 / 缺省规则模式：如果规则中的公式不都是句子的缺省规则。

  RECALL

  句子：任何变元都不是自由出现的公式。

  基项：不含自由变元的项。

• 闭规则：把一条开规则中的所有自由变元都替换为基项得到规则。

  e.g

  给定一条缺省规则模式$\varphi : \psi_1,\cdots, \psi_n/\chi$，则对于任意基代换$\theta$, 可得到闭规则：

  $$\delta\theta = \frac{\varphi\theta : \psi_1\theta,\cdots, \psi_n\theta}{\chi\theta}$$

由于闭规则由开规则得到，因此可将开规则看作是缺省规则模式：一条开规则表示一组缺省规则的集合。注意，这个集合可以是无穷的。

规范缺省规则

规范缺省规则：形如 $\varphi:\chi / \chi$ 的缺省条件与结论相同的缺省规则。

缺省理论

用一组缺省规则的集合来表示包含例外的知识；
用一组一阶逻辑公式的集合表示事实性知识。
二者组成一个缺省理论。

缺省理论：一个二元组$T = \lang W,D\rang$。

• $W$: 一阶逻辑公式集合，用于表示已知的或约定的事实集合；
• $D$：一个可数的缺省规则集合。特别地，当$D$中所有规则是闭规则时，称理论是闭理论。

e.g缺省理论的非单调性质

考虑理论$T = \lang W,D\rang$，其中 $D =\{\top:p/q\}, W = \empty$ 。显然$q$ 在 $T$ 中可推出。

现添入事实$\lnot p$使得$W' = \{\lnot p\},T' = \lang W',D\rang$。此时$q$不可从$T'$中推出，即新信息的加入使得已推出的结论被收回。

缺省逻辑的语义

给定一个缺省理论，其语义指的是可以接受或相信哪些语句。概括地说，被接受或相信的语句集合称为外延。

• 事实可以相信。
• 如果一条缺省规则在某个背景下可以被应用，那么它的结论可以相信。
• 一阶逻辑的演绎封闭性：如果相信了一组语句（事实，应用缺省规则而添加的结论），那么这组语句的所有演绎结论可以相信。
• 除上述三点不相信其他无关的语句。

外延的定义：via 不动点

为了避免在应用规则后产生不一致的结论，把背景设置为事实集合$W$是不合适的，还需要考虑在应用规则之后各条规则的结论对其他规则的缺省条件的影响。

在运用缺省规则时，指定一个语句集合 作为规则应用的背景。

缺省规则的应用

给定两个句子集合$\Phi$和$\Psi$，一条缺省规则 $\delta= \varphi : \psi_1,\cdots, \psi_n/\chi$。在$\Phi$下把 $\delta$ 应用于$\Psi$指：如果$\varphi\in\Psi$，且$\lnot\psi_1 \not\in \Phi, \cdots , \lnot\psi_n \not\in \Phi$，那么 $\chi\in\Psi$。当$\Phi = \Psi$时，我们也说把 $\delta$ 应用于$\Psi$。

• $\Phi$：用于检查规则可应用性时的缺省条件成立与否的句子集合。
• $\Psi$：可接受的语句集合。

给定一个缺省理论$T = \lang W,D\rang$和一组语句集合$\Phi$，通过应用所有缺省规则可得到一组可接受的语句集合$\Psi$。

极小扩充语句集合

设 $T = \lang W,D\rang$是一个缺省理论，$\Gamma$为关于$D$的一个算子。$\Gamma$ 作用于任意的语句集合 $\Phi$，产生满足下列三性质的极小语句集合 $\Gamma(\Phi)$：

1. $W \sube \Gamma(\Phi)$。
2. $Th(\Gamma(\Phi)) = \Gamma(\Phi)$，其中$Th(\Gamma(\Phi)) = \{ \phi | \Gamma (\Phi)\vdash \phi\}$。
3. 对于$D$中的任何缺省规则 $\delta = \varphi : \psi_1, \cdots, \psi_n/\chi$，在$\Phi$下把 $\delta$ 应用于 $\Gamma(\Phi)$，即：如果$\varphi\in\Psi$，且$\lnot\psi_1 \not\in \Phi, \cdots , \lnot\psi_n \not\in \Phi$，那么 $\chi\in\Psi$。

$Th$ 算子实质上是获得一个演绎闭包，这个闭包可能是无穷的。

外延的不动点

句子集合$E$是缺省理论$T = \lang W,D\rang$的一个外延当且仅当$E$是算子$\Gamma$的一个不动点，即 $\Gamma(E) = E$。

• 并非所有缺省理论都有外延。

  考虑理论$T_1 = \lang W_1,D_1\rang$，其中 $D_1 =\{\top:p/\lnot p\}, W_1 = \empty$ 。显然不存在关于$D$的$\Gamma$算子的不动点。反证法设存在不动点$E$，则考虑$\lnot p\in E$，依照定义$\lnot p\not\in E$；再考虑$p\in E$，则$\lnot p\in E$，均产生矛盾。故不动点不存在。

  外延的不存在表征着缺省规则的矛盾。

• 并非有外延的缺省理论只有唯一的外延。

  考虑理论$T_2 = \lang W_2,D_2\rang$，其中 $D_2 =\{\top:p/\lnot q,\top:q/\lnot r,\top:r/\lnot s\}, W_2 = \empty$ 。$T_2$有唯一的外延$\{\lnot q,\lnot s\}$

  考虑理论$T_3 = \lang W_3,D_3\rang$，其中 $D_3 =\{p\wedge q_1:r_1/r_1,p\wedge q_2:r_2/r_2\}$,$W_3 = \{p,q_1\wedge q_2,r_1 \leftrightarrow\lnot r_2\}$ 。则$Th(W_3\cup\{r_1\})$和$Th(W_3\cup\{r_2\})$均为$T_3$的外延。

Method使用外延的不动点求解外延：

1. 假设一个外延$E: W \sube E$。
2. 在$E$ 下 求解$\Gamma(E)$
3. 判断$E = \Gamma(E)$ ? 若是，则$E$是外延；若不是，则回到1.

准归纳

LEMMA 1

设$E$为一阶命题集，$T = \lang W,D\rang$为一闭理论。递归定义$E_i (i = 1, 2, \cdots)$ 如下：

$$\begin{align*} E_0 &= W\\ E_{i + 1} &= Th(E_i)\cup\{\chi|\frac{\varphi : \psi_1,\cdots, \psi_n}{\chi}\in D,\varphi \in E_i,\lnot\phi_j\not\in E,j = 1,2,\cdots,n\} \end{align*}$$

$E$是$D$的一个外延当且仅当$E = \cup_{i = 0}^{\infty}E_i$。

请注意对于缺省条件，$\lnot\psi_i \not \in E = \cup_{i = 0}^{\infty}E_i$ 而非$\lnot\psi_i\not\in E_i$。

本定理仍是一个对外延的判定方法。外延的不动点定义不是完全建构性的，因此，为了获得一个缺省理论的外延，需要假定可能的命题集合。

PROOF

从外延的性质入手证明以上方法得到的是该理论的一个外延。

1. 由$E_0 = W,E = \cup_{i = 0}^{\infty}E_i$ 知$W \sube E$。

LEMMA 2

闭缺省理论$T = \lang W,D\rang$有不一致的外延$E$，当且仅当$W$不一致。

PF 由$W \sube E$ 充分性显然。反之，若$E$不一致，$E$ 必包含一切命题，因而所有缺省规则均无用，因此由Lemma 1得$E = Th(W)$，$W$必不一致。

考虑理论$T_4 = \lang W_4,D_4\rang$，其中 $D_4 =\left\{p:r/r,q:s/s\right\}, W_4 = \left\{p\vee q,\lnot p,\lnot q\right\}$ 。$T_2$有唯一的外延$Th(W_4)$。演绎推理的形式化定义可知当前提为假时，任何结论均认为为真。注意，由于$W_4$是不一致的，对于$Th(W_4)$可知任何结论均为真，也即$Th(W_4)$包含一切问题。

LEMMA 3

任何规范缺省理论都有一个外延。

• 规范缺省理论： 所有缺省规则均为规范缺省规则的缺省理论。

外延的定义：via 操作

缺省规则的可应用性

缺省规则 $\delta = \varphi : \psi1, \cdots , \psi_n/\chi$ 可应用于一组命题集合 $E$, 当且仅当 $\varphi \in E$，而且 $\lnot \psi_1 \not\in E, \cdots ,\lnot\psi_n \not\in E$。

请区分缺省规则的可应用性和缺省规则的应用。

给定一个缺省理论$T = \lang W,D\rang$，则做出如下符号约定：

• 缺省规则序列 ：规则实施的顺序。
  • $\Pi = (\delta_0,\delta_1,\cdots)$。每条规则最多在$\Pi$中出现一次。
  • $\Pi[k] = (\delta_0,\delta_1,\cdots,\delta_{k - 1})$ ，其中$\delta_i$与 $\Pi$中的$\delta_i$含义相同。
• 实施$\Pi$中规则得到的结论集合：$In(\Pi) = Th(W\cup\{cons(\delta)|\delta \in \Pi\})$
• 实施$\Pi$中规则得到的不能为真的公式集合:$Out(\Pi) = \{\lnot \psi|\psi\in just(\delta),\delta\in\Pi\}$

过程

• $\Pi$是理论$T$的一个过程，当且仅当对于$\Pi$每条规则 $\delta_k,k \ge 0$，可把 $\delta_k$ 应用于$In(\Pi[k])$。
• $\Pi$是成功的，当且仅当 $In(\Pi) \cap Out(\Pi) = \empty$。
• $\Pi$是封闭的，当且仅当对于任意 $\delta \in D$，如果它可被应用于 $In(\Pi)$，则它在$\Pi$中。

外延与过程树

• 外延：$E$是缺省理论$T = \lang W,D\rang$ 的外延，当且仅当 存在一个成功且封闭的$T$的过程$\Pi$，使得$E = In(\Pi)$。

• 过程树：

  设$T$是一个缺省理论。$T$的过程树定义如下：

  • 树的每个节点：标记 $In$ 命题集合和 $Out$ 命题集合。
  • 根节点：$In(\Pi[0]) = Th(W), Out(\Pi[0]) = \empty$
  • 其他非根节点： $In,Out$ 命题集合取决于从根节点到该非根节点所应用的缺省规则。设 $\Pi[k] = (\delta_0, . . . , \delta_k)$ 为过程树中从根节点到某个非根节点的长度为 $k$ 的路径，则该非根节点的$In,Out$ 命题集合分别为 $In(\Pi[k]),Out(\Pi[k])$。
  • 从根节点到叶节点的路径：对应$T$的一个过程。一个过程是失败的，若其中存在一个节点，$In \cap Out \not = \empty$。

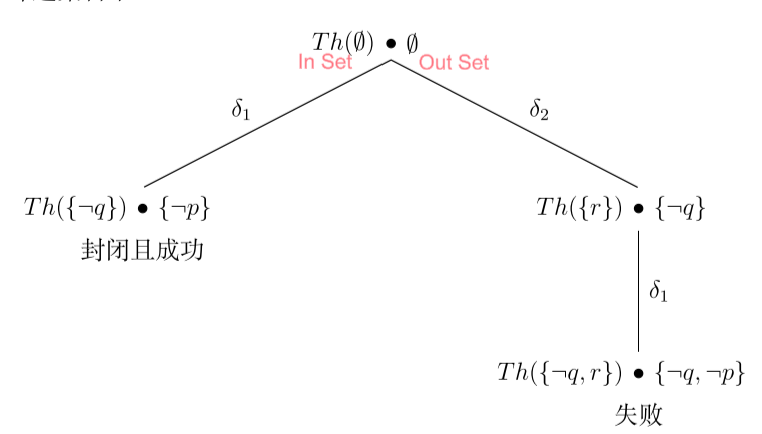
缺省证明

设$T=\lang W,D\rang$是一个规范缺省理论。称一阶命题 $\phi$ 有 $T$ 中的一个缺省证明，记作 $T\ |\!\!\!∼\phi$，如果存在 $D$ 的 有穷子集 的 有穷序列 $D_0,D_1, . . . , D_n$，使得：

• $W \cup cons(D_0) \vdash \phi$;
• 对于整数 $i: 1 \le i \le n$ 及 $pre(D_i−1)$ 中每一 $\varphi$，$W \cup cons(D_i) \vdash \varphi$。
• $D_n = \empty$
• $W \cup \cup^n_{i=0} cons(D_i)$ 是一致的。

RECALL

一条缺省规则可以被形式化地表示为：

$$\delta = \frac{\varphi : \psi_1,\cdots, \psi_n}{\chi}$$

或

$$\varphi : \psi_1,\cdots, \psi_n/\chi$$

其中

公式 $\varphi$	先决条件	$pre(\delta)$
公式$\psi_1,\cdots, \psi_n$	缺省条件	$just(\delta)$
$\chi$	结论	$cons(\delta)$

LEMMA 4

设$T=\lang W,D\rang$是一个规范缺省理论，$ϕ$ 为一阶命题。$T$ 中能推出 $\phi$( 即$T$ 中有含 $ϕ$ 的外延) 当且仅当 $ϕ$ 在 $T$ 中有一个缺省证明(即$T\ |\!\!\!∼\phi$)。

线性消解

设$T=\lang W,D\rang$是一个规范缺省理论。

• 规则$\delta$的结果子句：对于规则$\delta = \varphi : w/w \in D$，和子句$c_i \in w$，称 $(c_i, {\delta})$ 为 $\delta$ 的一个结果子句。
• 全体子句集合$S$:
  • $D$中所有规则的所有结果子句
  • $W$中命题的子句
  • 待证命题否定的子句

对$S$进行线性消解，知道导出空子句。在该过程中确定 $ϕ$ 的证明序列$D_0,D_1, . . . , D_n$。

线性消解方法 不可能是完备的。即可能有命题$A$，它虽为$T$的定理，但是不能用线性消解法获得$A$的证明。

结论: 怀疑的或轻信的

我们知道一个缺省理论可能有多个外延，而处于不同外延中的命题可能存在矛盾。设$T=\lang W,D\rang$是一个缺省理论，$\phi$是一阶命题，用$ext(T)$表示$T$所有外延的集合，则

• $T$ 怀疑推出 $\phi$: 当且仅当 $\forall E\in ext(T),\phi \in E$，即$\phi \in\cap_{E \in ext(T)}E$；
• $T$轻信推出 $\phi$：当且仅当 $\exist E\in ext(T),\phi \in E$，即 $\phi \in \cup_{E\in ext(T)}E$。